Various Activation Functions

What is an activation function ?

Let us consider a neuron, which outputs a weighted sum of the inputs plus some bias.

$Y = Sum(weight * input) + bias$

But here the value of Y can range from -infinity to +infinity. We do not know the bounds of the value. Here we need what we call an activation function which helps us to determine if that particular neuron can be activated (fired) or not.

It is just like any another function, which we use to get the output of any node. It is also called a Transfer function, used to transfer the input and map them to resultant values in the range of 0-1 or -1 to 1(depends on the function).

Activations functions can be linear or non-linear, but most widely used are non-linear activation functions.

Source - Google

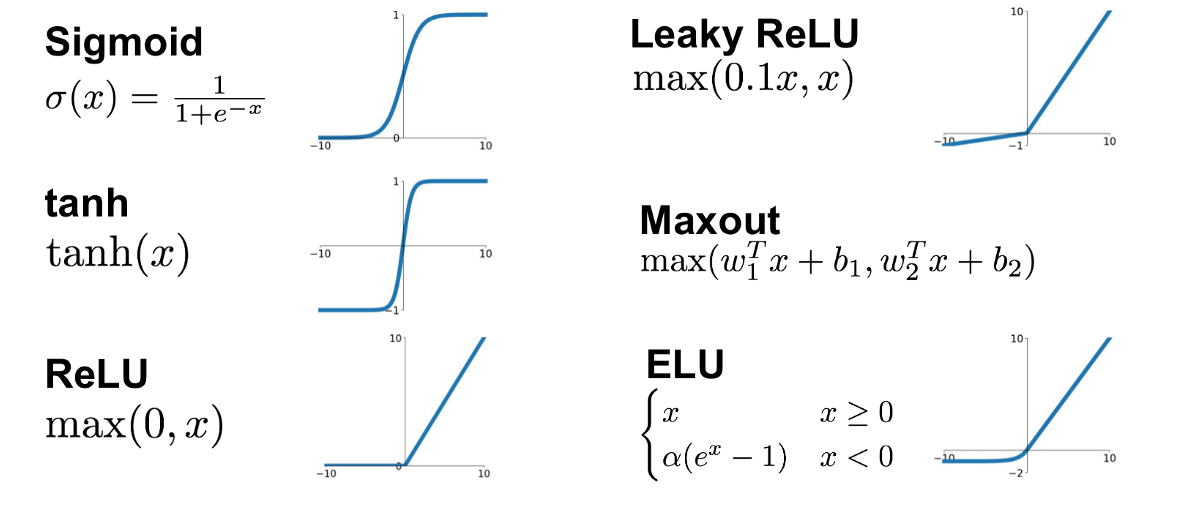
Selection of the activation function is mostly dependent on the problem and nature of the data. For example, sigmoid is suitable for networks where the output is in the range [0, 1]. However, the tanh and “sigmoid” activation functions saturate the neuron very fast and can vanish the gradient. Despite tanh, the non-zero centered output from sigmoid can cause unstable dynamics in the gradient updates for the weights. The ReLU activation function leads to sparser gradients and greatly accelerates the convergence of stochastic gradient descent (SGD) compared to the sigmoid or tanh activation functions. ReLU is computationally cheap, since it can be implemented by thresholding an activation value at zero. However, ReLU is not resistant against a large gradient flow and as the weight matrix grows, the neuron may remain inactive during training.